Fermi–Dirac Distribution for Non-interacting Fermions
The Fermi–Dirac distribution describes how particles are distributed over energy states in systems consisting of many identical particles that obey the Pauli exclusion principle.
The occupation number is directly proportional to the particle spin, and inversely proportional to 1 plus the exponential of the difference betweeen state energy and the chemical potential per mole times the number of moles, all divided by the Boltzmann constant and the temperature.
Formula
![Copy to Clipboard QuantityVariable[OverBar[Subscript["n", "i"]], "Unitless"] == (1 + 2*QuantityVariable["s", "Unitless"])/(1 + E^((Quantity[1, "BoltzmannConstant"^(-1)]*(-(QuantityVariable["n", "Amount"]*QuantityVariable["μ", "ChemicalPotential"]) + QuantityVariable[Subscript["E", "i"], "Energy"]))/QuantityVariable["T", "Temperature"]))](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/c41/c410802a-1620-461e-814c-865cb129defc/Webpage/FormulaImage.png)
Forms
Examples
Get the resource:
| In[1]:= |
| Out[1]= |  |
Get the formula:
| In[2]:= |
| Out[2]= | 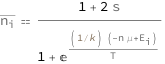 |
Use some values:
| In[3]:= |
| Out[3]= | 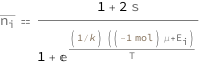 |