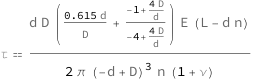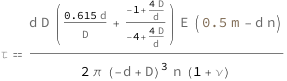Maximum Shear Stress in Spring
The maximum shear stress in a spring is the maximum shear stress the spring can suffer before permanent deformation.
The maximum shear stress in a spring increases linearly with the free length of a spring and its Young's modulus. It decreases with the Poisson ratio, the spring wire diameter, the number of active windings and the cube of the spring's outer diameter.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 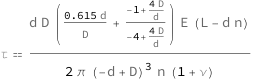 |
Use some values:
| Out[3]= | 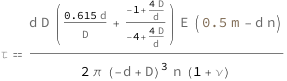 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["τ", "Stress"] == (QuantityVariable["d", "Diameter"]*QuantityVariable["D", "Diameter"]*((0.615*QuantityVariable["d", "Diameter"])/QuantityVariable["D", "Diameter"] + (-1 + (4*QuantityVariable["D", "Diameter"])/QuantityVariable["d", "Diameter"])/(-4 + (4*QuantityVariable["D", "Diameter"])/QuantityVariable["d", "Diameter"]))*QuantityVariable["E", "YoungsModulus"]*(QuantityVariable["L", "Length"] - QuantityVariable["d", "Diameter"]*QuantityVariable["n", "Unitless"]))/(2*Pi*(-QuantityVariable["d", "Diameter"] + QuantityVariable["D", "Diameter"])^3*QuantityVariable["n", "Unitless"]*(1 + QuantityVariable["ν", "PoissonRatio"]))](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/c09/c09e4ef4-737a-4cbf-9db5-3c7693bc3de6/Webpage/FormulaImage.png)