Probability of Exceedance
The frequency of exceedance, sometimes called the annual rate of exceedance, is the number of times in a certain period that a random process exceeds some critical value.
The average annual occurrences equal the number of times exceeded divided by the observed time period. The probability of exceedance equals 1 minus the exponential of the negative of the average annual occurrences times the prediction time period. The mean recurrance interval equals the reciprocal of the average annual occurrences.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 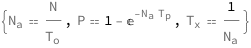 |
Use some values:
| Out[3]= | 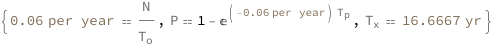 |
External Links
Publisher Information
![Copy to Clipboard {QuantityVariable[Subscript["N", "a"], "Frequency"] == QuantityVariable["N", "Unitless"]/QuantityVariable[Subscript["T", "o"], "Time"], QuantityVariable["P", "Unitless"] == 1 - E^(-(QuantityVariable[Subscript["N", "a"], "Frequency"]*QuantityVariable[Subscript["T", "p"], "Time"])), QuantityVariable[Subscript["T", "x"], "Time"] == QuantityVariable[Subscript["N", "a"], "Frequency"]^(-1)}](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/be8/be88ce0d-df75-476b-9ca2-f13f117bed20/Webpage/FormulaImage.png)
