Hohmann Angular Alignment
The Hohmann transfer orbit is an elliptical orbit used to transfer between two circular orbits of different radii in the same plane. The angular alignment is the bearing needed to make the transfer.
The Hohmann angular alignment is roughly proportional to the sum of 1 plus the ratio of the orbital radii of the inner and outer bodies to the 3/2 power.
Formula
![Copy to Clipboard QuantityVariable["α", "Angle"] == Pi*(1 - Sqrt[(1 + QuantityVariable[Subscript["r", "1"], "Length"]/QuantityVariable[Subscript["r", "2"], "Length"])^3]/(2*Sqrt[2]))](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/bc1/bc190339-f00a-4f8d-9e75-77c4aeb3963b/Webpage/FormulaImage.png)
| symbol | description | physical quantity |
|---|---|---|
| α | Hohmann angular alignment | "Angle" |
| r1 | orbital radius of inner body | "Length" |
| r2 | orbital radius of outer body | "Length" |
Forms
Examples
Get the resource:
| In[1]:= |
| Out[1]= |  |
Get the formula:
| In[2]:= |
| Out[2]= | 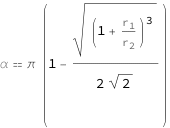 |
Use some values:
| In[3]:= |
| Out[3]= | 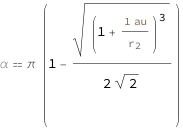 |