Larmor Frequency
The Larmor precession is the precession of the magnetic moment of an object about an external magnetic field. The Larmor frequency is the frequency of that procession.
The angular frequency for a Larmor precession equals the magnetic induction times the gyromagnetic ratio. The gyromagnetic ratio equals the g\[Hyphen]factor times the electric charge divided by twice the mass of the object. The frequency for a Larmor precession is the angular frequency divided by 2\[Pi].
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 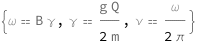 |
Use some values:
| Out[3]= |  |
External Links
Publisher Information
![Copy to Clipboard {QuantityVariable["ω", "AngularFrequency"] == QuantityVariable["B", "MagneticInduction"]*QuantityVariable["γ", "MagneticFrequencyShift"], QuantityVariable["γ", "MagneticFrequencyShift"] == (QuantityVariable["g", "Unitless"]*QuantityVariable["Q", "ElectricCharge"])/(2*QuantityVariable["m", "Mass"]), QuantityVariable["ν", "Frequency"] == QuantityVariable["ω", "AngularFrequency"]/(2*Pi)}](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/b91/b9181c97-44dd-4122-90b7-05d7491a7c85/Webpage/FormulaImage.png)

![FormulaData[
ResourceObject[
"Larmor Frequency"], {QuantityVariable["B","MagneticInduction"] ->
Quantity[1, "Teslas"],
QuantityVariable["g","Unitless"] -> 2.0023193043617`,
QuantityVariable["Q","ElectricCharge"] ->
Quantity[1.6000000000000002`*^-19, "Coulombs"]}]](images/b91/b9181c97-44dd-4122-90b7-05d7491a7c85-io-3-i.en.gif)
