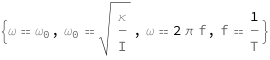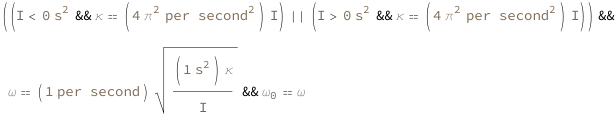Torsion Harmonic Oscillator
A torsion harmonic oscillator is a twisting system that, when displaced from its equilibrium position, experiences a restoring force proportional to the displacement.
The angular frequency for a torsion harmonic oscillator equals the natural angular frequency, as well as 2\[Pi] times the frequency. The frequency equals the reciprocal of the period. The natural frequency equals the square root of the torsional constant divided by the moment of inertia.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 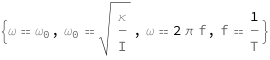 |
Use some values:
| Out[3]= | 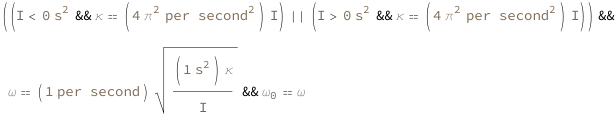 |
External Links
Publisher Information
![Copy to Clipboard {QuantityVariable["ω", "AngularFrequency"] == QuantityVariable[Subscript["ω", "0"], "AngularFrequency"], QuantityVariable[Subscript["ω", "0"], "AngularFrequency"] == Sqrt[QuantityVariable["κ", "TorsionalConstant"]/QuantityVariable["I", "MomentOfInertia"]], QuantityVariable["ω", "AngularFrequency"] == 2*Pi*QuantityVariable["f", "Frequency"], QuantityVariable["f", "Frequency"] == QuantityVariable["T", "Period"]^(-1)}](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/b8e/b8ee1ed5-0344-4b0d-9bb9-e72b8cc496c3/Webpage/FormulaImage.png)