Area Moment of Inertia of a Regular Hexagon about a Centroidal Axis
The second moment of area, also known as the moment of inertia of plane area, area moment of inertia or second area moment, is a geometrical property of an area that reflects how its points are distributed with regard to an arbitrary axis.
The second moment of area for a regular hexagon equals edge length to the fourth power multiplied by a constant factor.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 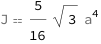 |
Use some values:
| Out[3]= | 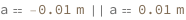 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["J", "SecondMomentOfArea"] == (5*Sqrt[3]*QuantityVariable["a", "Length"]^4)/16](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/b75/b75fac2a-13c2-45a0-a15d-6603578cbf72/Webpage/FormulaImage.png)

![FormulaData[
ResourceObject[
"Area Moment of Inertia of a Regular Hexagon about a Centroidal \
Axis"], {QuantityVariable["J","SecondMomentOfArea"] ->
Quantity[0.541266`, ("Centimeters")^4]}]](images/b75/b75fac2a-13c2-45a0-a15d-6603578cbf72-io-3-i.en.gif)