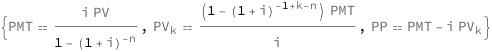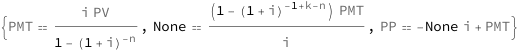Principal and Interest Using Principal Part
Principal is the amount on which the issuer pays interest, and which, most commonly, has to be repaid at the end of the term.
The payment increases with the interest rate (per period) and the initial loan amount, and decreases with the number of compounding periods. The present value at the beginning of period k increases with the payment and decreases with the interest rate (per period). The present value of the loan decreases the closer k is to the number of compounding periods. The principal portion of the payment equals the payment minus the interest rate per period times the present value at the beginning of period k.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 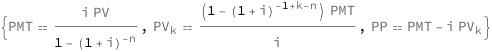 |
Use some values:
| Out[3]= | 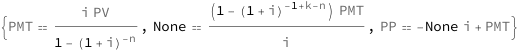 |
External Links
Publisher Information
![Copy to Clipboard {QuantityVariable["PMT", "Money"] == (QuantityVariable["i", "Unitless"]*QuantityVariable["PV", "Money"])/(1 - (1 + QuantityVariable["i", "Unitless"])^(-QuantityVariable["n", "Unitless"])), QuantityVariable[Subscript["PV", "k"], "Unitless"] == ((1 - (1 + QuantityVariable["i", "Unitless"])^(-1 + QuantityVariable["k", "Unitless"] - QuantityVariable["n", "Unitless"]))*QuantityVariable["PMT", "Money"])/QuantityVariable["i", "Unitless"], QuantityVariable["PP", "Money"] == QuantityVariable["PMT", "Money"] - QuantityVariable["i", "Unitless"]*QuantityVariable[Subscript["PV", "k"], "Unitless"]}](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/b56/b568c9c8-1e3a-40dd-9110-20079d6fbeb7/Webpage/FormulaImage.png)