Modified Internal Rate of Return
The modified internal rate of return is a financial measure of an investment's attractiveness.
The modified internal rate of return increases with a net-positive value of positive cash flows and the reinvestment rate. Increasing values of the net-positive value of negative cash flows and finance rate decrease it. The number of time periods also affects the modified internal rate of return.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 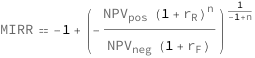 |
Use some values:
| Out[3]= | 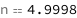 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["MIRR", "Unitless"] == -1 + (-((QuantityVariable[Subscript["NPV", "pos"], "Money"]*(1 + QuantityVariable[Subscript["r", "R"], "Unitless"])^QuantityVariable["n", "Unitless"])/(QuantityVariable[Subscript["NPV", "neg"], "Money"]*(1 + QuantityVariable[Subscript["r", "F"], "Unitless"]))))^(-1 + QuantityVariable["n", "Unitless"])^(-1)](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/b43/b43e219c-c53b-471e-a5f0-24321fbae562/Webpage/FormulaImage.png)


![FormulaData[
ResourceObject["Modified Internal Rate of Return"], {QuantityVariable[
\!\(\*SubscriptBox[\("r"\), \("R"\)]\),"Unitless"] ->
Quantity[12, "Percent"], QuantityVariable[
\!\(\*SubscriptBox[\("r"\), \("F"\)]\),"Unitless"] ->
Quantity[10, "Percent"], QuantityVariable[
\!\(\*SubscriptBox[\("NPV"\), \("neg"\)]\),"Money"] ->
Quantity[-200, "USDollars"], QuantityVariable[
\!\(\*SubscriptBox[\("NPV"\), \("pos"\)]\),"Money"] ->
Quantity[500, "USDollars"],
QuantityVariable["MIRR","Unitless"] -> 0.4147`}]](images/b43/b43e219c-c53b-471e-a5f0-24321fbae562-io-3-i.en.gif)