Drake Equation
The Drake equation is a probabilistic argument used to arrive at an estimate of the number of active, communicative extraterrestrial civilizations in the Milky Way galaxy.
The number of communicating civilizations in the Milky Way equals the product of the rate of star formation in the Milky Way, the fraction of stars with planets, the average number of Earth\[Hyphen]like planets per star with planets, the fraction of Earth\[Hyphen]like planets that develop life, the fraction of life\[Hyphen]bearing planets that develop intelligent life, the fraction of civilizations that communicate and the average lifetime of communicating civilizations.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 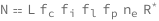 |
Use some values:
| Out[3]= | 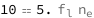 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["N", "Unitless"] == QuantityVariable["L", "Time"]*QuantityVariable[Subscript["f", "c"], "Unitless"]*QuantityVariable[Subscript["f", "i"], "Unitless"]*QuantityVariable[Subscript["f", "l"], "Unitless"]*QuantityVariable[Subscript["f", "p"], "Unitless"]*QuantityVariable[Subscript["n", "e"], "Unitless"]*QuantityVariable[SuperStar["R"], "Frequency"]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/b3d/b3d9dee2-b3f7-46fb-80a9-1ee8e6d3a2f6/Webpage/FormulaImage.png)
