Moment of Inertia of a Thin Disk
The mass moment of inertia measures the extent to which an object resists rotational acceleration about a particular axis, and is the rotational analog to mass. For a disk of infinitesimal thickness, the moments of inertia are taken to be about the axes passing through the disk's center of mass.
The parallel moment of inertia is half the mass times the radius squared. The perpendicular moment of inertia is a quarter of the mass times the radius squared.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 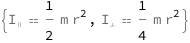 |
Use some values:
| Out[3]= | 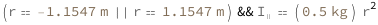 |
External Links
Publisher Information
![Copy to Clipboard {QuantityVariable[Subscript["I", "∥"], "MomentOfInertia"] == (QuantityVariable["m", "Mass"]*QuantityVariable["r", "Radius"]^2)/2, QuantityVariable[Subscript["I", "⊥"], "MomentOfInertia"] == (QuantityVariable["m", "Mass"]*QuantityVariable["r", "Radius"]^2)/4}](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/b20/b20823c6-01ba-452f-9ebb-dc879066fa44/Webpage/FormulaImage.png)

![FormulaData[
ResourceObject[
"Moment of Inertia of a Thin Disk"], {QuantityVariable[
"m","Mass"] -> Quantity[1, "Kilograms"], QuantityVariable[
\!\(\*SubscriptBox[\("I"\), \("\[UpTee]"\)]\),"MomentOfInertia"] ->
Quantity[0.3333333333333333`, "Kilograms" ("Meters")^2]}]](images/b20/b20823c6-01ba-452f-9ebb-dc879066fa44-io-3-i.en.gif)