Wolfram Computation Meets Knowledge

Wolfram Formula Repository (Under Development)

Black Hole Event Horizon Area with Angular Momentum

An event horizon is a boundary in spacetime beyond which events cannot affect an outside observer.

The event horizon area increases roughly quadratically with the mass and the angular momentum.

Formula

QuantityVariable["A", "Area"] == 4*Pi*((Quantity[1, "SpeedOfLight"^(-2)]*QuantityVariable["J", "AngularMomentum"]^2)/QuantityVariable["M", "Mass"]^2 + (Quantity[1, "GravitationalConstant"/"SpeedOfLight"^2]*QuantityVariable["M", "Mass"] + Sqrt[(Quantity[-1, "SpeedOfLight"^(-2)]*QuantityVariable["J", "AngularMomentum"]^2)/QuantityVariable["M", "Mass"]^2 + Quantity[1, "GravitationalConstant"^2/"SpeedOfLight"^4]*QuantityVariable["M", "Mass"]^2])^2)

symbol description physical quantity
A event horizon area "Area"
J angular momentum "AngularMomentum"
M mass "Mass"

Forms

Examples

Get the resource:

In[1]:=
ResourceObject["Black Hole Event Horizon Area with Angular Momentum"]
Out[1]=

Get the formula:

In[2]:=
FormulaData[ ResourceObject[ "Black Hole Event Horizon Area with Angular Momentum"]]
Out[2]=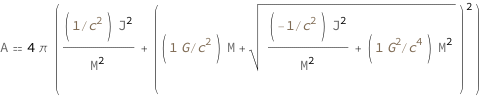

Use some values:

In[3]:=
FormulaData[ ResourceObject[ "Black Hole Event Horizon Area with Angular Momentum"], \ {QuantityVariable["J","AngularMomentum"] -> Quantity[1.`*^-10, "Joules" "Seconds"], QuantityVariable["M","Mass"] -> Quantity[2.`*^30, "Kilograms"]}]
Out[3]=

Publisher Information