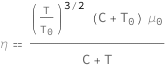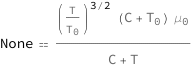Sutherland's Formula
Sutherland's formula can be used to derive the dynamic viscosity of an ideal gas as a function of the temperature.
The dynamic viscosity equals the product of the sum of Sutherland's constant and the reference temperature divided by the sum of Sutherland's constant and the temperature, the reference viscosity and the ratio to the 3/2 power of the temperature to reference temperature.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 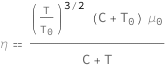 |
Use some values:
| Out[3]= | 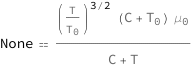 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["η", "DynamicViscosity"] == ((QuantityVariable["T", "Temperature"]/QuantityVariable[Subscript["T", "0"], "Temperature"])^(3/2)*(QuantityVariable["C", "Temperature"] + QuantityVariable[Subscript["T", "0"], "Temperature"])*QuantityVariable[Subscript["μ", "0"], "DynamicViscosity"])/(QuantityVariable["C", "Temperature"] + QuantityVariable["T", "Temperature"])](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/aee/aee90a74-388b-432e-8958-8f0aeeb5f443/Webpage/FormulaImage.png)