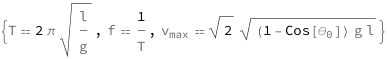Small-Oscillation Pendulum
A simple pendulum is an isolated system that assumes a massless, inextensible and taut cord; a point mass weight at the end, with motion occurring only in two dimensions; no friction or air resistance; a uniform gravitational field; and a fixed support. A small-oscillation pendulum assumes a small initial angle.
The period increases with the square root of the length divided by gravitational acceleration. The frequency equals the reciprocal of the period. The maximum speed is proportional to the square root of the product of the gravitational acceleration, length of the pendulum and 1 minus the cosine of the initial angle.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 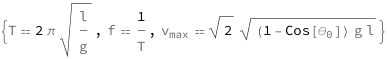 |
Use some values:
| Out[3]= | 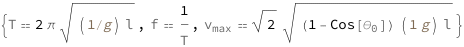 |
External Links
Publisher Information
![Copy to Clipboard {QuantityVariable["T", "Period"] == 2*Pi*Sqrt[QuantityVariable["l", "Length"]/QuantityVariable["g", "GravitationalAcceleration"]], QuantityVariable["f", "Frequency"] == QuantityVariable["T", "Period"]^(-1), QuantityVariable[Subscript["v", "max"], "Speed"] == Sqrt[2]*Sqrt[(1 - Cos[QuantityVariable[Subscript["θ", "0"], "Angle"]])*QuantityVariable["g", "GravitationalAcceleration"]*QuantityVariable["l", "Length"]]}](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/ae0/ae0efd4e-e81b-471e-8c69-a3bcd0771708/Webpage/FormulaImage.png)