Area Moment of Inertia of an Annulus about a Centroidal Axis
The second moment of area, also known as moment of inertia of plane area, area moment of inertia or second area moment, is a geometrical property of an area that reflects how its points are distributed with regard to an arbitrary axis.
The second moment of area for an annulus equals the difference between the fourth powers of the inner and outer radius multiplied by \[Pi] divided by four.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 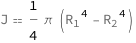 |
Use some values:
| Out[3]= | 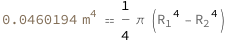 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["J", "SecondMomentOfArea"] == (Pi*(QuantityVariable[Subscript["R", "1"], "Radius"]^4 - QuantityVariable[Subscript["R", "2"], "Radius"]^4))/4](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/a80/a804dd60-c61e-4f07-8036-b03bce9ff745/Webpage/FormulaImage.png)

![FormulaData[
ResourceObject[
"Area Moment of Inertia of an Annulus about a Centroidal Axis"], \
{QuantityVariable["J","SecondMomentOfArea"] ->
Quantity[0.0460194`, ("Meters")^4]}]](images/a80/a804dd60-c61e-4f07-8036-b03bce9ff745-io-3-i.en.gif)