Seismic Moment Using Rupture Area
Seismic moment is a quantity used by seismologists to measure the size of an earthquake.
Seismic moment equals the product of the rupture area, the shear modulus and the average displacement on rupture. The seismic moment magnitude is proportional to the logarithm of the seismic moment.
Formula
![Copy to Clipboard {QuantityVariable[Subscript["M", "0"], "Energy"] == QuantityVariable["A", "Area"]*QuantityVariable["μ", "ShearModulus"]*QuantityVariable[OverBar["D"], "Length"], QuantityVariable[Subscript["M", "w"], "Unitless"] == (2*(-9.1 + Log[Quantity[1, "Joules"^(-1)]*QuantityVariable[Subscript["M", "0"], "Energy"]]/Log[10]))/3}](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/a77/a7731d09-bea5-4659-a24c-87a25ef27483/Webpage/FormulaImage.png)
| symbol | description | physical quantity |
|---|---|---|
| M0 | seismic moment | "Energy" |
| A | rupture area | "Area" |
| μ | shear modulus | "ShearModulus" |
| D̅ | average displacement on rupture | "Length" |
| Mw | seismic moment magnitude | "Unitless" |
Forms
Examples
Get the resource:
| In[1]:= |
| Out[1]= |  |
Get the formula:
| In[2]:= |
| Out[2]= | 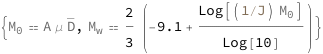 |
Use some values:
| In[3]:= |
| Out[3]= | 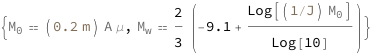 |