Speed of Sound in an Ideal Gas by Pressure
The speed of sound is the distance traveled per unit time by a sound wave as it propagates through an elastic medium.
The speed of sound equals the square root of the product of the pressure and the adiabatic index divided by the mass density.
Formula
![Copy to Clipboard QuantityVariable[Subscript["v", "s"], "Speed"] == Sqrt[(QuantityVariable["P", "Pressure"]*QuantityVariable["γ", "Unitless"])/QuantityVariable["d", "MassDensity"]]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/a51/a511fa44-e5bc-426a-97f5-98469d28d365/Webpage/FormulaImage.png)
| symbol | description | physical quantity |
|---|---|---|
| vs | speed of sound | "Speed" |
| d | density | "MassDensity" |
| P | pressure | "Pressure" |
| γ | adiabatic index | "Unitless" |
Forms
Examples
Get the resource:
| In[1]:= |
| Out[1]= |  |
Get the formula:
| In[2]:= |
| Out[2]= |  |
Use some values:
| In[3]:= |
| Out[3]= | 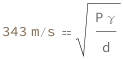 |