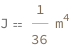Area Moment of Inertia of a Filled Triangle about a Centroidal Axis
The second moment of area, also known as moment of inertia of plane area, area moment of inertia or second area moment, is a geometrical property of an area that reflects how its points are distributed with regard to an arbitrary axis.
The second moment of area for a filled triangle equals the product of the base and height to the third power divided by 36.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 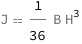 |
Use some values:
| Out[3]= | 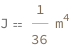 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["J", "SecondMomentOfArea"] == (QuantityVariable["B", "Length"]*QuantityVariable["H", "Height"]^3)/36](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/a22/a22530b4-0728-4dc4-a86f-b94f4fe34964/Webpage/FormulaImage.png)

![FormulaData[
ResourceObject[
"Area Moment of Inertia of a Filled Triangle about a Centroidal \
Axis"], {QuantityVariable["B","Length"] -> Quantity[1, "Meters"],
QuantityVariable["H","Height"] -> Quantity[1, "Meters"]}]](images/a22/a22530b4-0728-4dc4-a86f-b94f4fe34964-io-3-i.en.gif)