Destructive Thin-Film Interference
Thin-film interference is a natural phenomenon in which light waves reflected by the upper and lower boundaries of a thin film interfere with one another, either enhancing or reducing the reflected light. When the thickness of the film is an odd multiple of one quarter-wavelength of the light on it, the reflected waves from both surfaces interfere to cancel each other. Since the wave cannot be reflected, it is completely transmitted instead.
Twice the thickness equals the product of the order, the wavelength and the index of refraction of the outside medium divided by the index of refraction of the thin film.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 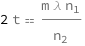 |
Use some values:
| Out[3]= | 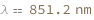 |
External Links
Publisher Information
![Copy to Clipboard 2*QuantityVariable["t", "Thickness"] == (QuantityVariable["m", "Unitless"]*QuantityVariable["λ", "Wavelength"]*QuantityVariable[Subscript["n", "1"], "Unitless"])/QuantityVariable[Subscript["n", "2"], "Unitless"]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/a11/a1114183-4f82-49c2-92da-bc61046e81b6/Webpage/FormulaImage.png)
