Freezing-Point Depression Equation Using Solvent Properties
Freezing-point depression is the process in which adding a solute to a solvent decreases the freezing point of the solvent.
The freezing-point depression equals the product of the molar gas constant, solvent molar mass, solvent freezing point squared and solution molarity divided by the solvent molar enthalpy of fusion.
Formula
![Copy to Clipboard QuantityVariable[Subscript["ΔT", "f"], "TemperatureDifference"] == (Quantity[1, "MolarGasConstant"]*QuantityVariable["m", "Molality"]*QuantityVariable["M", "MolarMass"]*QuantityVariable[Subscript["T", "f"], "Temperature"]^2)/QuantityVariable[Subscript["ΔH", "fus"], "MolarEnergy"]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/a09/a09f9f9d-be99-4f80-a58d-2d4421c0694c/Webpage/FormulaImage.png)
| symbol | description | physical quantity |
|---|---|---|
| ΔTf | freezing point depression | "TemperatureDifference" |
| m | solution molality | "Molality" |
| M | solvent molar mass | "MolarMass" |
| Tf | solvent freezing point | "Temperature" |
| ΔHfus | solvent molar enthalpy of fusion | "MolarEnergy" |
Forms
Examples
Get the resource:
| In[1]:= |
| Out[1]= |  |
Get the formula:
| In[2]:= |
| Out[2]= | 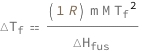 |
Use some values:
| In[3]:= | ![FormulaData[
ResourceObject[
"Freezing-Point Depression Equation Using Solvent Properties"], \
{QuantityVariable[
\!\(\*SubscriptBox[\("T"\), \("f"\)]\),"Temperature"] ->
Quantity[0.`, "DegreesCelsius"]}]](images/a09/a09f9f9d-be99-4f80-a58d-2d4421c0694c-io-3-i.en.gif) |
| Out[3]= | 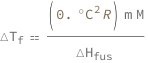 |