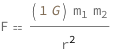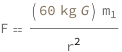Newton's Law of Universal Gravitation
Newton's law of universal gravitation states that a particle attracts every other particle in the universe using a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centers.
The gravitational force equals the product of the gravitational constant, the mass of the objects involved and the reciprocal of the square of the distance between them.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 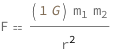 |
Use some values:
| Out[3]= | 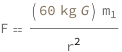 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["F", "Force"] == (Quantity[1, "GravitationalConstant"]*QuantityVariable[Subscript["m", "1"], "Mass"]*QuantityVariable[Subscript["m", "2"], "Mass"])/QuantityVariable["r", "Distance"]^2](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/a06/a06896b7-93d7-4052-b0b5-26e3ba3fd60c/Webpage/FormulaImage.png)