Dean Number
The Dean number is a dimensionless group in fluid mechanics, which occurs in the study of flow in curved pipes and channels.
The Dean number is proportional to the square root of the cube of the diameter, the characteristic speed, the mass density, the reciprocal of the square root of the radius of curvature and the reciprocal of the dynamic viscosity.
Formula
![Copy to Clipboard QuantityVariable["De", "DeanNumber"] == (QuantityVariable["d", "Diameter"]*Sqrt[QuantityVariable["d", "Diameter"]/QuantityVariable["R", "RadiusOfCurvature"]]*QuantityVariable["v", "Speed"]*QuantityVariable["ρ", "MassDensity"])/(Sqrt[2]*QuantityVariable["η", "DynamicViscosity"])](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/a00/a00fcc35-2397-44d5-9306-0d0f1915f963/Webpage/FormulaImage.png)
| symbol | description | physical quantity |
|---|---|---|
| De | Dean number | "DeanNumber" |
| d | diameter | "Diameter" |
| R | radius of curvature | "RadiusOfCurvature" |
| v | characteristic speed | "Speed" |
| η | dynamic viscosity | "DynamicViscosity" |
| ρ | mass density | "MassDensity" |
Forms
Examples
Get the resource:
| In[1]:= |
| Out[1]= |  |
Get the formula:
| In[2]:= |
| Out[2]= | 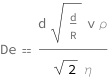 |
Use some values:
| In[3]:= |
| Out[3]= | 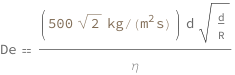 |