Speed of Sound in an Ideal Gas by Temperature and Mass of Molecule
The speed of sound is the distance traveled per unit time by a sound wave as it propagates through an elastic medium.
The speed of sound equals the square root of the product of the Boltzmann constant, temperature and adiabatic index divided by the mass of a molecule.
Formula
![Copy to Clipboard QuantityVariable[Subscript["v", "s"], "Speed"] == Sqrt[(Quantity[1, "BoltzmannConstant"]*QuantityVariable["T", "Temperature"]*QuantityVariable["γ", "Unitless"])/QuantityVariable["m", "Mass"]]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/9dd/9dd4005f-a7a5-49d8-a4aa-0d3f2af9072c/Webpage/FormulaImage.png)
| symbol | description | physical quantity |
|---|---|---|
| vs | speed of sound | "Speed" |
| m | mass of a molecule | "Mass" |
| T | temperature | "Temperature" |
| γ | adiabatic index | "Unitless" |
Forms
Examples
Get the resource:
| In[1]:= |
| Out[1]= |  |
Get the formula:
| In[2]:= |
| Out[2]= | 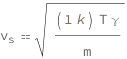 |
Use some values:
| In[3]:= | ![FormulaData[
ResourceObject[
"Speed of Sound in an Ideal Gas by Temperature and Mass of \
Molecule"], {QuantityVariable["T","Temperature"] ->
Quantity[300, "Kelvins"]}]](images/9dd/9dd4005f-a7a5-49d8-a4aa-0d3f2af9072c-io-3-i.en.gif) |
| Out[3]= | 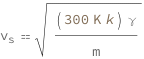 |