Rainbow Altitude
A rainbow is a meteorological phenomenon that is caused by reflection, refraction and dispersion of light in water droplets, resulting in a spectrum of light appearing in the sky. It takes the form of a multicolored arc. Rainbows caused by sunlight always appear in the section of sky directly opposite the Sun. The altitude of the top edge of the primary bow depends on the index of refraction and the Sun's position.
The altitude of the rainbow depends on the index of refraction of the droplets and the position of the Sun. As the index of refraction increases, the angles of incidence, refraction and deviation approach 0, and thus the altitude becomes the negative of the altitude of the Sun. As the index of refraction approaches 1, the angles of incidence and refraction approaches one-half \[Pi] radians. The angle of deviation approaches \[Pi] radians, making the altitude roughly that of the Sun but opposite the zenith.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 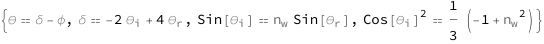 |
Use some values:
| Out[3]= | 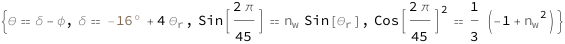 |
External Links
Publisher Information
![Copy to Clipboard {QuantityVariable["θ", "Angle"] == QuantityVariable["δ", "Angle"] - QuantityVariable["ϕ", "Angle"], QuantityVariable["δ", "Angle"] == -2*QuantityVariable[Subscript["θ", "i"], "Angle"] + 4*QuantityVariable[Subscript["θ", "r"], "Angle"], Sin[QuantityVariable[Subscript["θ", "i"], "Angle"]] == QuantityVariable[Subscript["n", "w"], "Unitless"]*Sin[QuantityVariable[Subscript["θ", "r"], "Angle"]], Cos[QuantityVariable[Subscript["θ", "i"], "Angle"]]^2 == (-1 + QuantityVariable[Subscript["n", "w"], "Unitless"]^2)/3}](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/d51/d51551a2-dccc-4790-a65e-15824993d935/Webpage/FormulaImage.png)
