Wolfram Computation Meets Knowledge

Wolfram Formula Repository (Under Development)

Jeans Length Using Speed of Sound

The Jeans length is the critical radius for instability of a collapsing thermalized cloud of self­gravitating gas.

The Jeans length is proportional to the sound speed times the square root of the reciprocal of the mass density.

Formula

QuantityVariable[Subscript["R", "J"], "Length"] == Sqrt[Pi]*QuantityVariable["c", "SoundSpeed"]*Sqrt[Quantity[1, "GravitationalConstant"^(-1)]/QuantityVariable["ρ", "MassDensity"]]

symbol description physical quantity
RJ Jeans length "Length"
c sound speed "SoundSpeed"
ρ mass density "MassDensity"

Forms

Examples

Get the resource:

In[1]:=
ResourceObject["Jeans Length Using Speed of Sound"]
Out[1]=

Get the formula:

In[2]:=
FormulaData[ResourceObject["Jeans Length Using Speed of Sound"]]
Out[2]=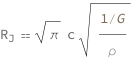

Use some values:

In[3]:=
FormulaData[ ResourceObject[ "Jeans Length Using Speed of Sound"], {QuantityVariable[ "c","SoundSpeed"] -> Quantity[3129.28`6., ("Meters")/("Seconds")], QuantityVariable[ \!\(\*SubscriptBox[\("R"\), \("J"\)]\),"Length"] -> Quantity[2.624`4.*^14, "Kilometers"]}]
Out[3]=

Source Metadata

  • Creator:
  • Date: 1902

Publisher Information