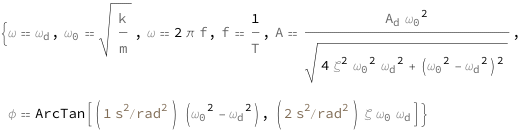Damped Driven Spring Harmonic Oscillator
A spring harmonic oscillator is a spring that, when displaced from its equilibrium position, experiences a restoring force proportional to the displacement. A damped driven spring harmonic oscillator experiences a frictional force (damping) proportional to the velocity, as well as an external time-dependent force driving the system.
The angular frequency for a damped driven harmonic oscillator equals the driving angular frequency as well as 2\[Pi] times the frequency. The frequency equals the reciprocal of the period. The amplitude is directly proportional to the driving amplitude, and maximizes when the natural angular frequency equals the driving frequency. The damping ratio decreases the amplitude. The phase depends on the difference between the natural angular frequency and driving frequency, adjusted by the damping ratio. The natural angular frequency equals the square root of the ratio between the spring constant and the mass.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 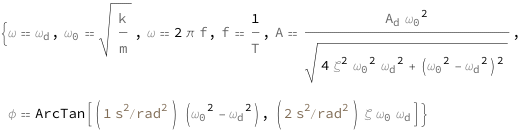 |
Use some values:
| Out[3]= |  |
External Links
Publisher Information
![Copy to Clipboard {QuantityVariable["ω", "AngularFrequency"] == QuantityVariable[Subscript["ω", "d"], "AngularFrequency"], QuantityVariable[Subscript["ω", "0"], "AngularFrequency"] == Sqrt[QuantityVariable["k", "SpringConstant"]/QuantityVariable["m", "Mass"]], QuantityVariable["ω", "AngularFrequency"] == 2*Pi*QuantityVariable["f", "Frequency"], QuantityVariable["f", "Frequency"] == QuantityVariable["T", "Period"]^(-1), QuantityVariable["A", "Unitless"] == (QuantityVariable[Subscript["A", "d"], "Unitless"]*QuantityVariable[Subscript["ω", "0"], "AngularFrequency"]^2)/Sqrt[4*QuantityVariable["ζ", "Unitless"]^2*QuantityVariable[Subscript["ω", "0"], "AngularFrequency"]^2*QuantityVariable[Subscript["ω", "d"], "AngularFrequency"]^2 + (QuantityVariable[Subscript["ω", "0"], "AngularFrequency"]^2 - QuantityVariable[Subscript["ω", "d"], "AngularFrequency"]^2)^2], QuantityVariable["ϕ", "Angle"] == ArcTan[Quantity[1, "Seconds"^2/"Radians"^2]*(QuantityVariable[Subscript["ω", "0"], "AngularFrequency"]^2 - QuantityVariable[Subscript["ω", "d"], "AngularFrequency"]^2), Quantity[2, "Seconds"^2/"Radians"^2]*QuantityVariable["ζ", "Unitless"]*QuantityVariable[Subscript["ω", "0"], "AngularFrequency"]*QuantityVariable[Subscript["ω", "d"], "AngularFrequency"]]}](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/c65/c65c6d89-cc15-4523-b0bd-23603548fef3/Webpage/FormulaImage.png)