Birthday Problem Approximation
The birthday problem, or birthday paradox, concerns the probability that, in a set of n randomly chosen people, some pair of them will have the same birthday.
The probability that m people will have the same birthday depends nonlinearly on k, the total number of people and the number of possible birthdays.
Formula
![QuantityVariable["n", "Person"]/E^(QuantityVariable["n", "Person"]/(QuantityVariable["d", "Unitless"]*QuantityVariable["k", "Person"])) == (QuantityVariable["k", "Person"]!*Log[(1 - QuantityVariable["p", "Unitless"])^(-1)]*QuantityVariable["d", "Unitless"]^(-1 + QuantityVariable["k", "Person"])*(1 - QuantityVariable["n", "Person"]/(QuantityVariable["d", "Unitless"]*(1 + QuantityVariable["k", "Person"]))))^QuantityVariable["k", "Person"]^(-1)](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/c92/c9233575-078a-426a-9077-8bf7bc2e852d/Webpage/FormulaImage.png "Copy to Clipboard")
Forms
Examples
Get the resource:
| In[1]:= | ![ResourceObject["Birthday Problem Approximation"]](images/c92/c9233575-078a-426a-9077-8bf7bc2e852d-io-1-i.en.gif){kind=small} |
| Out[1]= |  |
Get the formula:
| In[2]:= | ![FormulaData[ResourceObject["Birthday Problem Approximation"]]](images/c92/c9233575-078a-426a-9077-8bf7bc2e852d-io-2-i.en.gif){kind=small} |
| Out[2]= |  |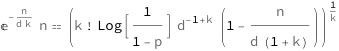
Use some values:
| In[3]:= | ![FormulaData[
ResourceObject[
"Birthday Problem Approximation"], {QuantityVariable[
"n","Person"] -> 23}]](images/c92/c9233575-078a-426a-9077-8bf7bc2e852d-io-3-i.en.gif){kind=small} |
| Out[3]= | 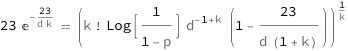 |