Diffraction Intensity Ratio for Circular Aperture Diffraction
The diffraction intensity ratio is the ratio between intensity at a given angle and the incident intensity of light passing through a circular aperture.
The diffraction intensity ratio depends on the wavelength, diffraction angle and radius of the circular aperture.
Formula
![Copy to Clipboard QuantityVariable[Subscript[Style["I", Italic], "θ"]/Subscript[Style["I", Italic], "0"], "Unitless"] == (BesselJ[1, (2*Pi*QuantityVariable["a", "Distance"]*Sin[QuantityVariable["θ", "Angle"]])/QuantityVariable["λ", "Wavelength"]]^2*Csc[QuantityVariable["θ", "Angle"]]^2*QuantityVariable["λ", "Wavelength"]^2)/(Pi^2*QuantityVariable["a", "Distance"]^2)](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/9a0/9a035269-66d3-4c61-97aa-feb0ea703be4/Webpage/FormulaImage.png)
| symbol | description | physical quantity |
|---|---|---|
| Iθ/I0 | normalized transmitted intensity | "Unitless" |
| a | aperture radius | "Distance" |
| λ | wavelength | "Wavelength" |
| θ | diffraction angle | "Angle" |
Forms
Examples
Get the resource:
| In[1]:= |
| Out[1]= |  |
Get the formula:
| In[2]:= |
| Out[2]= | 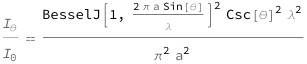 |
Use some values:
| In[3]:= |
| Out[3]= | 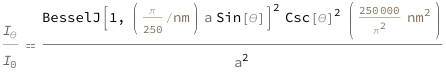 |