Differential Bending of a Bimetallic Strip
A bimetallic strip is used to convert a temperature change into mechanical displacement. The differential bending of a bimetallic strip describes the radius of curvature as a function of temperature and the length and properties of the materials used.
The radius of curvature of a bimetallic strip increases directly with the change in temperature and the difference in the thermal expansion coefficients of the materials used. The Young's modulus and the height of the strips also contribute to the change in a nonlinear fashion with increasing heights diminishing the radius of curvature.
Formula
![Copy to Clipboard QuantityVariable["κ", "Curvature"] == (6*QuantityVariable["ΔT", "TemperatureDifference"]*QuantityVariable[Subscript["E", "1"], "YoungsModulus"]*QuantityVariable[Subscript["E", "2"], "YoungsModulus"]*QuantityVariable[Subscript["H", "1"], "Height"]*QuantityVariable[Subscript["H", "2"], "Height"]*(QuantityVariable[Subscript["H", "1"], "Height"] + QuantityVariable[Subscript["H", "2"], "Height"])*(QuantityVariable[Subscript["α", "1"], "LinearThermalExpansionCoefficient"] - QuantityVariable[Subscript["α", "2"], "LinearThermalExpansionCoefficient"]))/(QuantityVariable[Subscript["E", "1"], "YoungsModulus"]^2*QuantityVariable[Subscript["H", "1"], "Height"]^4 + 4*QuantityVariable[Subscript["E", "1"], "YoungsModulus"]*QuantityVariable[Subscript["E", "2"], "YoungsModulus"]*QuantityVariable[Subscript["H", "1"], "Height"]^3*QuantityVariable[Subscript["H", "2"], "Height"] + 6*QuantityVariable[Subscript["E", "1"], "YoungsModulus"]*QuantityVariable[Subscript["E", "2"], "YoungsModulus"]*QuantityVariable[Subscript["H", "1"], "Height"]^2*QuantityVariable[Subscript["H", "2"], "Height"]^2 + 4*QuantityVariable[Subscript["E", "1"], "YoungsModulus"]*QuantityVariable[Subscript["E", "2"], "YoungsModulus"]*QuantityVariable[Subscript["H", "1"], "Height"]*QuantityVariable[Subscript["H", "2"], "Height"]^3 + QuantityVariable[Subscript["E", "2"], "YoungsModulus"]^2*QuantityVariable[Subscript["H", "2"], "Height"]^4)](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/948/948d0b92-469b-4971-8ed0-46b6438561f4/Webpage/FormulaImage.png)
Forms
Examples
Get the resource:
| In[1]:= |
| Out[1]= |  |
Get the formula:
| In[2]:= |
| Out[2]= |
Use some values:
| In[3]:= | ![FormulaData[
ResourceObject[
"Differential Bending of a Bimetallic Strip"], {QuantityVariable[
\!\(\*SubscriptBox[\("H"\), \("1"\)]\),"Height"] ->
Quantity[0.1`, "Meters"], QuantityVariable[
\!\(\*SubscriptBox[\("\[Alpha]"\), \("1"\)]\),
"LinearThermalExpansionCoefficient"] ->
Quantity[0.000018999999999999998`, 1/("KelvinsDifference")],
QuantityVariable["\[Kappa]","Curvature"] ->
Quantity[0.00439234`, 1/("Meters")]}]](images/948/948d0b92-469b-4971-8ed0-46b6438561f4-io-3-i.en.gif) |
| Out[3]= | 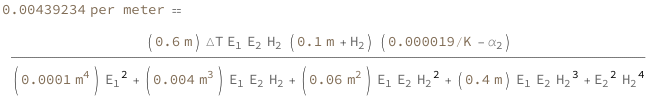 |