Dittus–Boelter Equation
The Dittus–Boelter equation (for turbulent flow) is an explicit function for calculating the Nusselt number. The Nusselt number is the ratio of convective to conductive heat transfer across (normal to) the boundary.
The Nusselt number is proportional to the Prandtl number for heat transfer to the heating exponent times the Reynolds number to the four-fifths power.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 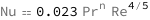 |
Use some values:
| Out[3]= | 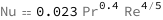 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["Nu", "NusseltNumberHeatTransfer"] == 0.023*QuantityVariable["Pr", "PrandtlNumberHeatTransfer"]^QuantityVariable["n", "Unitless"]*QuantityVariable["Re", "ReynoldsNumber"]^(4/5)](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/8d4/8d479fc6-ddeb-4780-a1b6-d7884fc687ef/Webpage/FormulaImage.png)
