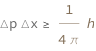Heisenberg Uncertainty Principle for Position and Momentum
The uncertainty principle, also known as Heisenberg's uncertainty principle or Heisenberg's indeterminacy principle, is any of a variety of mathematical inequalities asserting a fundamental limit to the precision with which certain pairs of physical properties of a particle, known as complementary variables, can be known.
The product of the measured momentum uncertainty and measured position uncertainty is greater than or equal to the Planck constant divided by 4\[Pi].
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 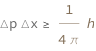 |
Use some values:
| Out[3]= | 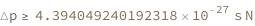 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["Δp", "Momentum"]*QuantityVariable["Δx", "Distance"] >= Quantity[1/(4*Pi), "PlanckConstant"]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/8d2/8d2af077-5179-4f33-a8b5-38baf647b144/Webpage/FormulaImage.png)