Torricelli's Theorem
Torricelli's law, also known as Torricelli's theorem, is a theorem in fluid dynamics relating the speed of fluid flowing out of an orifice to the height of fluid above the opening. The law states that the speed of efflux of a fluid through a sharp-edged hole at the bottom of a tank filled to a depth is the same as the speed that a body (in this case, a drop of water) would acquire in falling freely from a height.
The speed of efflux from the hole is proportional to the square root of the acceleration of gravity times the difference between the height of fluid in the vessel and the height of the efflux point from the base.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 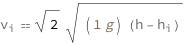 |
Use some values:
| Out[3]= | 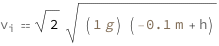 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable[Subscript["v", "i"], "Speed"] == Sqrt[2]*Sqrt[Quantity[1, "StandardAccelerationOfGravity"]*(QuantityVariable["h", "Height"] - QuantityVariable[Subscript["h", "i"], "Height"])]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/8bc/8bc2a516-aa2c-4f33-8616-598c3812a768/Webpage/FormulaImage.png)
