Simple Boiling-Point Elevation Equation
Boiling-point elevation describes the phenomenon that the boiling point of a liquid (a solvent) will be higher when another compound is added, meaning that a solution has a higher boiling point than a pure solvent. This formula assumes dilute ideal nonvolatile solutions.
Boiling-point elevation equals the solution molality times the ebullioscopic constant.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 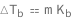 |
Use some values:
| Out[3]= | 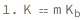 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable[Subscript["ΔT", "b"], "TemperatureDifference"] == QuantityVariable["m", "Molality"]*QuantityVariable[Subscript["K", "b"], "MolalBoilingPointElevationConstant"]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/8b4/8b41c2ba-1d6b-4d61-993b-f9383130394a/Webpage/FormulaImage.png)
