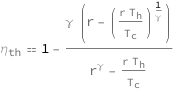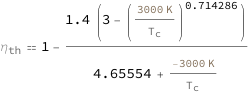Atkinson Cycle
The Atkinson-cycle engine is a type of internal combustion engine invented by James Atkinson in 1882. The Atkinson cycle is designed to provide efficiency at the expense of power density, or total power extracted per unit of displacement per rotation. A variation of this approach is used in some modern automobile engines.
The thermal efficiency of an Atkinson-cycle engine using an ideal gas depends on the heat capacity ratio, compression ratio and ratios of the high and low temperatures in a nonlinear fashion.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 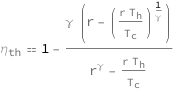 |
Use some values:
| Out[3]= | 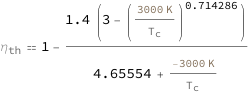 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable[Subscript["η", "th"], "ThermalEfficiency"] == 1 - (QuantityVariable["γ", "HeatCapacityRatio"]*(QuantityVariable["r", "Unitless"] - ((QuantityVariable["r", "Unitless"]*QuantityVariable[Subscript["T", "h"], "Temperature"])/QuantityVariable[Subscript["T", "c"], "Temperature"])^QuantityVariable["γ", "HeatCapacityRatio"]^(-1)))/(QuantityVariable["r", "Unitless"]^QuantityVariable["γ", "HeatCapacityRatio"] - (QuantityVariable["r", "Unitless"]*QuantityVariable[Subscript["T", "h"], "Temperature"])/QuantityVariable[Subscript["T", "c"], "Temperature"])](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/8b2/8b2aca3c-2910-4f2c-a4ae-b46f3b7851cf/Webpage/FormulaImage.png)