Manning Formula
The Manning formula is an empirical formula estimating the average velocity of a liquid flowing in a conduit that does not completely enclose the liquid, such as open-channel flow.
The flow velocity of the fluid increases with the square root of the hydraulic grade line slope and the flow area to the two-thirds power. It decreases inversely with the wetted perimeter to the two-thirds power and the Manning's roughness coefficient. The flow rate equals the flow area times the flow velocity of the fluid.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 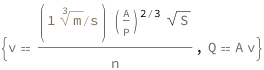 |
Use some values:
| Out[3]= | 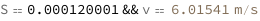 |
External Links
Publisher Information
![Copy to Clipboard {QuantityVariable["v", "Speed"] == (Quantity[1, "Meters"^(1/3)/"Seconds"]*(QuantityVariable["A", "Area"]/QuantityVariable["P", "Length"])^(2/3)*Sqrt[QuantityVariable["S", "Unitless"]])/QuantityVariable["n", "ManningRoughnessCoefficient"], QuantityVariable["Q", "VolumeFlow"] == QuantityVariable["A", "Area"]*QuantityVariable["v", "Speed"]}](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/881/881fa5d3-2948-43de-b6d9-e13020328adc/Webpage/FormulaImage.png)

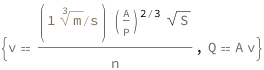
![FormulaData[
ResourceObject[
"Manning Formula"], {QuantityVariable["P","Length"] ->
Quantity[9.5`, "Meters"],
QuantityVariable["Q","VolumeFlow"] ->
Quantity[1218.12`, ("Meters")^3/("Seconds")],
QuantityVariable["A","Area"] -> Quantity[202.5`, ("Meters")^2],
QuantityVariable["n","ManningRoughnessCoefficient"] -> 0.014`}]](images/881/881fa5d3-2948-43de-b6d9-e13020328adc-io-3-i.en.gif)