Bose–Einstein Distribution for Non-interacting Bosons

The BoseEinstein distribution describes the occupancy of an energy state within a BoseEinstein condensate.

The occupancy number of a states of a Bose\[Hyphen]Einstein condensate depends on the particle spin, the chamical potential, the energy of the state, the temperature and the amount of material present.

Formula

QuantityVariable[OverBar[Subscript["n", "i"]], "Unitless"] == (1 + 2*QuantityVariable["s", "Unitless"])/(-1 + E^((Quantity[1, "BoltzmannConstant"^(-1)]*(-(QuantityVariable["n", "Amount"]*QuantityVariable["μ", "ChemicalPotential"]) + QuantityVariable[Subscript["E", "i"], "Energy"]))/QuantityVariable["T", "Temperature"]))

symbol	description	physical quantity
n i̅	occupation number	"Unitless"
T	temperature	"Temperature"
n	amount	"Amount"
μ	chemical potential	"ChemicalPotential"
E_i	state energy	"Energy"
s	particle spin	"Unitless"

Forms

Examples

Open in Wolfram Cloud

Download Example Notebook

Get the resource:

In[1]:=

$ResourceObject["Bose\[Dash]Einstein Distribution for Non-interacting \ Bosons"]$

Out[1]=

Get the formula:

In[2]:=

$FormulaData[ ResourceObject[ "Bose\[Dash]Einstein Distribution for Non-interacting Bosons"]]$

Out[2]=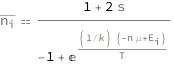

Use some values:

In[3]:=

$FormulaData[ ResourceObject[ "Bose\[Dash]Einstein Distribution for Non-interacting Bosons"], \ {QuantityVariable["\[Mu]","ChemicalPotential"] -> Quantity[0, ("AvogadroNumber" "Electronvolts")/("Moles")]}]$

Out[3]=

Wolfram Formula Repository (Under Development)

Bose–Einstein Distribution for Non-interacting Bosons

Formula

Forms

Examples

External Links

Source Metadata

Publisher Information