Bethe Formula
The Bethe formula describes the mean energy loss per distance traveled of swift-charged particles (protons, alpha particles, atomic ions) traversing matter (or, alternatively, the stopping power of the material).
The Bethe formula shows how the stopping power declines with speed electric charge and electron density.
Formula
![Copy to Clipboard QuantityVariable["-dE/dx", "LinearStoppingPower"] == (Quantity[1/(4*Pi), "ElementaryCharge"^5/("ElectricConstant"^2*"ElectronMass"*"SpeedOfLight")]*QuantityVariable["n", "InverseVolume"]*(Log[(Quantity[2, "ElectronMass"]*QuantityVariable["v", "Speed"]^2)/(QuantityVariable["I", "Energy"]*(1 + Quantity[-1, "SpeedOfLight"^(-2)]*QuantityVariable["v", "Speed"]^2))] + Quantity[-1, "SpeedOfLight"^(-2)]*QuantityVariable["v", "Speed"]^2))/(QuantityVariable["Q", "ElectricCharge"]*QuantityVariable["v", "Speed"])](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/86c/86c67499-f032-4019-bcbb-78390b7a97e7/Webpage/FormulaImage.png)
Forms
Examples
Get the resource:
| In[1]:= |
| Out[1]= |  |
Get the formula:
| In[2]:= |
| Out[2]= | 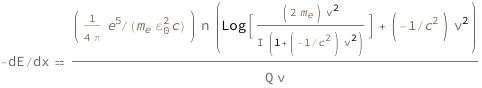 |
Use some values:
| In[3]:= |
| Out[3]= | 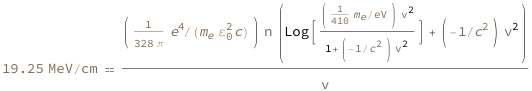 |