Spherical Law of Tangents
The spherical law of tangents is a statement about the relationship between the tangents of two angles of a triangle on a sphere and the angular lengths of the opposing sides.
The cotangent of the average of the angular lengths of first and second sides times the tangent of half the difference between the angular lengths of the first and second sides equals the cotangent of the average of the angles opposite the first and second sides times the tangent of half the difference between the angles opposite the first and second sides.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 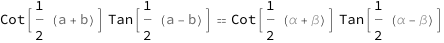 |
Use some values:
| Out[3]= | 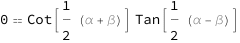 |
External Links
Publisher Information
![Copy to Clipboard Cot[(QuantityVariable["a", "Angle"] + QuantityVariable["b", "Angle"])/2]*Tan[(QuantityVariable["a", "Angle"] - QuantityVariable["b", "Angle"])/2] == Cot[(QuantityVariable["α", "Angle"] + QuantityVariable["β", "Angle"])/2]*Tan[(QuantityVariable["α", "Angle"] - QuantityVariable["β", "Angle"])/2]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/858/85843fb7-9b6c-434f-beea-4c98ee830f9f/Webpage/FormulaImage.png)
