Richter Scale Magnitude
The Richter magnitude scale assigns a magnitude number to quantify the size of an earthquake. The Richter scale is a base 10 logarithmic scale, which defines magnitude as the logarithm of the ratio of the amplitude of the seismic waves to an arbitrary, minor amplitude, as recorded on a standardized seismograph at a standard distance.
The Richter scale magnitude is proportional to the logarithm of the maximum trace amplitude plus the distance from station to hypocenter.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 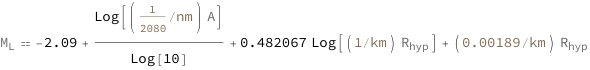 |
Use some values:
| Out[3]= |  |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable[Subscript["M", "L"], "Unitless"] == -2.09 + Log[Quantity[1/2080, "Nanometers"^(-1)]*QuantityVariable["A", "Distance"]]/Log[10] + 0.4820668749126095*Log[Quantity[1, "Kilometers"^(-1)]*QuantityVariable[Subscript["R", "hyp"], "Distance"]] + Quantity[0.00189, "Kilometers"^(-1)]*QuantityVariable[Subscript["R", "hyp"], "Distance"]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/858/8581e944-a7e4-427c-a2de-8a37ccf47613/Webpage/FormulaImage.png)