Wolfram Computation Meets Knowledge

Wolfram Formula Repository (Under Development)

Eccentricity of an Ellipse

An ellipse is a curve in a plane surrounding two focal points such that the sum of the distances to the two focal points is constant for every point on the curve. The shape of an ellipse (how \"elongated\" it is) is represented by its eccentricity, which for an ellipse can be any number from 0 (the limiting case of a circle) to arbitrarily close to but less than 1.

The eccentricity of an ellipse equals the square root of the difference between the squares of the semimajor and semiminor axes divided by the semimajor axis.

Formula

QuantityVariable["e", "Unitless"] == Sqrt[QuantityVariable["a", "Length"]^2 - QuantityVariable["b", "Length"]^2]/QuantityVariable["a", "Length"]

symbol description physical quantity
e eccentricity "Unitless"
a semimajor axis "Length"
b semiminor axis "Length"

Forms

Examples

Get the resource:

In[1]:=
ResourceObject["Eccentricity of an Ellipse"]
Out[1]=

Get the formula:

In[2]:=
FormulaData[ResourceObject["Eccentricity of an Ellipse"]]
Out[2]=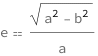

Use some values:

In[3]:=
FormulaData[ ResourceObject[ "Eccentricity of an Ellipse"], {QuantityVariable["b","Length"] -> 4, QuantityVariable["e","Unitless"] -> 0.6`}]
Out[3]=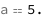

Publisher Information