Thermal Doppler Broadening of Wavelength
Doppler broadening is the broadening of spectral lines due to the Doppler effect, caused by a distribution of thermal velocities of atoms or molecules.
Doppler broadening increases with the square of the temperature, inversely with the square of the mass and directly with the source wavelength.
Formula
![Copy to Clipboard {QuantityVariable[Subscript["σ", "λ"], "Wavelength"] == Sqrt[(Quantity[1, "BoltzmannConstant"/"SpeedOfLight"^2]*QuantityVariable["T", "Temperature"])/QuantityVariable["m", "Mass"]]*QuantityVariable[Subscript["λ", "s"], "Wavelength"], QuantityVariable[Row[{"Δ", Subscript["λ", "FWHM"]}], "Wavelength"] == 2*Sqrt[2*Log[2]]*Sqrt[(Quantity[1, "BoltzmannConstant"/"SpeedOfLight"^2]*QuantityVariable["T", "Temperature"])/QuantityVariable["m", "Mass"]]*QuantityVariable[Subscript["λ", "s"], "Wavelength"]}](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/809/80934020-56d1-49c0-a5a1-d21eff489918/Webpage/FormulaImage.png)
| symbol | description | physical quantity |
|---|---|---|
| σλ | standard deviation | "Wavelength" |
| m | mass of a particle | "Mass" |
| T | temperature | "Temperature" |
| λs | wavelength at the source | "Wavelength" |
| ΔλFWHM | wavelength full width at half-maximum | "Wavelength" |
Forms
Examples
Get the resource:
| In[1]:= |
| Out[1]= |  |
Get the formula:
| In[2]:= |
| Out[2]= | 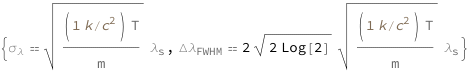 |
Use some values:
| In[3]:= | ![FormulaData[
ResourceObject[
"Thermal Doppler Broadening of Wavelength"], {QuantityVariable[
Row[{"\[CapitalDelta]",
\!\(\*SubscriptBox[\("\[Lambda]"\), \("FWHM"\)]\)}],"Wavelength"] ->
Quantity[3.53`, "Picometers"]}]](images/809/80934020-56d1-49c0-a5a1-d21eff489918-io-3-i.en.gif) |
| Out[3]= | 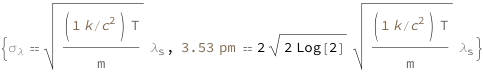 |