Wolfram Computation Meets Knowledge

Wolfram Formula Repository (Under Development)

Area Moment of Inertia of a Filled Trapezoid about a Centroidal Axis

The second moment of area, also known as moment of inertia of plane area, area moment of inertia or second area moment, is a geometrical property of an area that reflects how its points are distributed with regard to an arbitrary axis.

The second moment of area for a filled trapezoid increases cubically with the height and roughly linearly with the lengths of the bases.

Formula

QuantityVariable["J", "SecondMomentOfArea"] == (QuantityVariable["H", "Height"]^3*(QuantityVariable["B", "Length"]^2 + 4*QuantityVariable["B", "Length"]*QuantityVariable[Subscript["b", "2"], "Length"] + QuantityVariable[Subscript["b", "2"], "Length"]^2))/(36*(QuantityVariable["B", "Length"] + QuantityVariable[Subscript["b", "2"], "Length"]))

Forms

Examples

Get the resource:

In[1]:=
ResourceObject["Area Moment of Inertia of a Filled Trapezoid about a \ Centroidal Axis"]
Out[1]=

Get the formula:

In[2]:=
FormulaData[ ResourceObject[ "Area Moment of Inertia of a Filled Trapezoid about a Centroidal \ Axis"]]
Out[2]=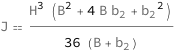

Use some values:

In[3]:=
FormulaData[ ResourceObject[ "Area Moment of Inertia of a Filled Trapezoid about a Centroidal \ Axis"], {QuantityVariable["J","SecondMomentOfArea"] -> Quantity[0.0833333`, ("Meters")^4], QuantityVariable[ \!\(\*SubscriptBox[\("b"\), \("2"\)]\),"Length"] -> Quantity[1, "Meters"], QuantityVariable["H","Height"] -> Quantity[1, "Meters"]}]
Out[3]=

Source Metadata

  • Contributor:

Publisher Information