Wolfram Computation Meets Knowledge

Wolfram Formula Repository (Under Development)

Jeans Mass Using Speed of Sound

The Jeans mass is the mass that a spherical cloud of interstellar gas must have in order to contract under its own weight.

The Jeans mass is proportional to the sound speed cubed divided by the square root of the mass density.

Formula

QuantityVariable[Subscript["M", "J"], "Mass"] == (Quantity[Pi/6, "GravitationalConstant"^(-3/2)]*QuantityVariable["c", "SoundSpeed"]^3)/Sqrt[QuantityVariable["ρ", "MassDensity"]]

symbol description physical quantity
MJ Jeans mass "Mass"
c sound speed "SoundSpeed"
ρ mass density "MassDensity"

Forms

Examples

Get the resource:

In[1]:=
ResourceObject["Jeans Mass Using Speed of Sound"]
Out[1]=

Get the formula:

In[2]:=
FormulaData[ResourceObject["Jeans Mass Using Speed of Sound"]]
Out[2]=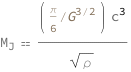

Use some values:

In[3]:=
FormulaData[ ResourceObject[ "Jeans Mass Using Speed of Sound"], {QuantityVariable[ "\[Rho]","MassDensity"] -> Quantity[6.69489`6.*^-24, ("Kilograms")/("Centimeters")^3], QuantityVariable[ \!\(\*SubscriptBox[\("M"\), \("J"\)]\),"Mass"] -> Quantity[1.`1., "Kilograms"]}]
Out[3]=

Source Metadata

  • Creator:
  • Date: 1902

Publisher Information