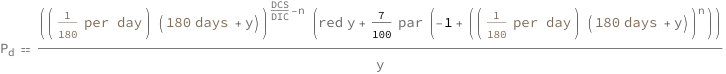Bond Dirty Price between Regular Coupon Payments
The dirt price of a bond is the value of a bond, including accrued interest since issue or the most recent coupon payment.
The dirty price of a bond depends on the remaining time on the current coupon, the number of coupons remaining, the rate and frequency of coupons, the face value of the bond, its redemption value and the annual yield.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= |  |
Use some values:
| Out[3]= | 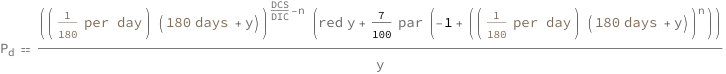 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable[Subscript["P", "d"], "Money"] == (((QuantityVariable["f", "Time"] + QuantityVariable["y", "Unitless"])/QuantityVariable["f", "Time"])^(QuantityVariable["DCS", "Time"]/QuantityVariable["DIC", "Time"] - QuantityVariable["n", "Unitless"])*(QuantityVariable["red", "Money"]*QuantityVariable["y", "Unitless"] + QuantityVariable["i", "Unitless"]*QuantityVariable["par", "Money"]*(-1 + ((QuantityVariable["f", "Time"] + QuantityVariable["y", "Unitless"])/QuantityVariable["f", "Time"])^QuantityVariable["n", "Unitless"])))/QuantityVariable["y", "Unitless"]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/7c7/7c7a014c-fb32-4c01-89ed-217c11344239/Webpage/FormulaImage.png)