Fresnel Equations for S-Polarized Light
The Fresnel equations calculate the reflection and transmission coefficients for light incident on an interface between media of differing refractive indices.
The transmission coefficient for s\[Hyphen]polarized incident light equals 1 minus the reflection coefficient. The reflection coefficient depends on the angle of incidence and the indices of refraction of the two media.
Formula
![Copy to Clipboard {QuantityVariable[Subscript["R", "s"], "Unitless"] == (Cos[QuantityVariable[Subscript["θ", "1"], "Angle"]]*QuantityVariable[Subscript["n", "1"], "Unitless"] - QuantityVariable[Subscript["n", "2"], "Unitless"]*Sqrt[1 - (QuantityVariable[Subscript["n", "1"], "Unitless"]^2*Sin[QuantityVariable[Subscript["θ", "1"], "Angle"]]^2)/QuantityVariable[Subscript["n", "2"], "Unitless"]^2])^2/(Cos[QuantityVariable[Subscript["θ", "1"], "Angle"]]*QuantityVariable[Subscript["n", "1"], "Unitless"] + QuantityVariable[Subscript["n", "2"], "Unitless"]*Sqrt[1 - (QuantityVariable[Subscript["n", "1"], "Unitless"]^2*Sin[QuantityVariable[Subscript["θ", "1"], "Angle"]]^2)/QuantityVariable[Subscript["n", "2"], "Unitless"]^2])^2, QuantityVariable[Subscript["T", "s"], "Unitless"] == 1 - QuantityVariable[Subscript["R", "s"], "Unitless"]}](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/7ae/7aee48d4-b987-464c-a13a-5bfbeb35c305/Webpage/FormulaImage.png)
Forms
Examples
Get the resource:
| In[1]:= |
| Out[1]= |  |
Get the formula:
| In[2]:= |
| Out[2]= | 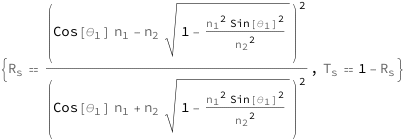 |
Use some values:
| In[3]:= |
| Out[3]= | 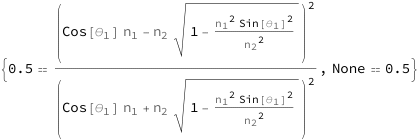 |