Ellipsoid Volume
An ellipsoid is a surface that may be obtained from a sphere by deforming it by means of directional scalings, or more generally, of an affine transformation.
The volume of an ellipsoid equals four-thirds \[Pi] times the product of the semiaxes.
Formula
![Copy to Clipboard QuantityVariable["V", "Volume"] == (4*Pi*QuantityVariable["a", "Length"]*QuantityVariable["b", "Length"]*QuantityVariable["c", "Length"])/3](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/781/78112949-a63d-498a-8df6-2033d3d7555a/Webpage/FormulaImage.png)
| symbol | description | physical quantity |
|---|---|---|
| V | volume | "Volume" |
| a | first semiaxis | "Length" |
| b | second semiaxis | "Length" |
| c | third semiaxis | "Length" |
Forms
Examples
Get the resource:
| In[1]:= |
| Out[1]= |  |
Get the formula:
| In[2]:= |
| Out[2]= |
Use some values:
| In[3]:= |
| Out[3]= | 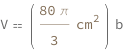 |