Rolling Motion
Rolling is a type of motion that combines rotation (commonly of an axially symmetric object) and translation of that object with respect to a surface (either one or the other moves), such that, if ideal conditions exist, the two are in contact with each other without sliding.
The kinetic energy of a rolling object equals half the mass times the speed squared plus half the moment of inertia times the angular frequency squared. The speed equals the object's radius times the angular frequency.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 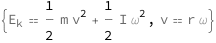 |
Use some values:
| Out[3]= | 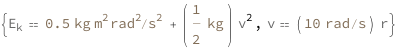 |
External Links
Publisher Information
![Copy to Clipboard {QuantityVariable[Subscript["E", "k"], "Energy"] == (QuantityVariable["m", "Mass"]*QuantityVariable["v", "Speed"]^2)/2 + (QuantityVariable["I", "MomentOfInertia"]*QuantityVariable["ω", "AngularFrequency"]^2)/2, QuantityVariable["v", "Speed"] == QuantityVariable["r", "Radius"]*QuantityVariable["ω", "AngularFrequency"]}](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/77b/77b887f0-1dc5-462a-9368-777b4226522e/Webpage/FormulaImage.png)