Mohr's Circle Plane Normal Strain X Direction
Mohr's circle is a two-dimensional graphical representation of the transformation law for the Cauchy stress tensor. Normal strain is a description of deformation in terms of relative displacement of particles in the normal direction in the body that excludes rigid-body motions.
The normal strain in a new x direction increases with the normal strains in the x and y directions (though a larger normal strain in the x direction will increase it more). Increased shear strain in the x\[Hyphen]y coordinates will also increase normal strain in the new x direction. The angle of the new x direction also modifies the normal strain in the new x direction.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 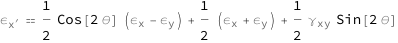 |
Use some values:
| Out[3]= | 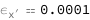 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable[Subscript["ε", Superscript["x", "′"]], "Unitless"] == (Cos[2*QuantityVariable["θ", "Angle"]]*(QuantityVariable[Subscript["ε", "x"], "Unitless"] - QuantityVariable[Subscript["ε", "y"], "Unitless"]))/2 + (QuantityVariable[Subscript["ε", "x"], "Unitless"] + QuantityVariable[Subscript["ε", "y"], "Unitless"])/2 + (QuantityVariable[Subscript["γ", "xy"], "Unitless"]*Sin[2*QuantityVariable["θ", "Angle"]])/2](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/77b/77b54959-b1e3-4fb2-a9be-eb09f3103b46/Webpage/FormulaImage.png)
