Maximum Spring Force
The maximum spring force is the maximum force the spring can exert before permanent deformation.
The maximum spring force increases linearly with the free length of a spring, spring wire diameter and its Young's modulus. It decreases with the Poisson ratio, the number of active windings and the cube of the spring outer diameter.
Formula
![Copy to Clipboard QuantityVariable[Subscript["F", "max"], "Force"] == (QuantityVariable["d", "Diameter"]^4*QuantityVariable["E", "YoungsModulus"]*(QuantityVariable["L", "Length"] - QuantityVariable["d", "Diameter"]*QuantityVariable["n", "Unitless"]))/(16*(-QuantityVariable["d", "Diameter"] + QuantityVariable["D", "Diameter"])^3*QuantityVariable["n", "Unitless"]*(1 + QuantityVariable["ν", "PoissonRatio"]))](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/75f/75f8f29f-b12e-41e6-9c95-8fcc62aed511/Webpage/FormulaImage.png)
| symbol | description | physical quantity |
|---|---|---|
| Fmax | maximum spring force | "Force" |
| d | spring wire diameter | "Diameter" |
| D | spring outer diameter | "Diameter" |
| E | Young's modulus | "YoungsModulus" |
| n | number of active windings | "Unitless" |
| L | free length of spring | "Length" |
| ν | Poisson ratio | "PoissonRatio" |
Forms
Examples
Get the resource:
| In[1]:= |
| Out[1]= |  |
Get the formula:
| In[2]:= |
| Out[2]= | 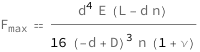 |
Use some values:
| In[3]:= |
| Out[3]= | 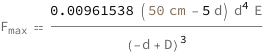 |