Boussinesq Approximation Parameter Using Fluid Densities
The Boussinesq approximation is used in the field of buoyancy-driven flow (also known as natural convection). It ignores density differences except where they appear in terms multiplied by the acceleration due to gravity. The essence of the Boussinesq approximation is that the difference in inertia is negligible, but gravity is sufficiently strong to make the specific weight appreciably different between the two fluids.
The Boussinesq approximation parameter increases as the difference between the cold and hot water densities increases. As the reference fluid density increases, the parameter inversely declines.
Examples
Get the resource:
| Out[1]= |  |
Get the formula:
| Out[2]= | 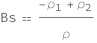 |
Use some values:
| Out[3]= | 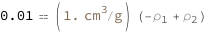 |
External Links
Publisher Information
![Copy to Clipboard QuantityVariable["Bs", "BoussinesqApproximationParameter"] == (-QuantityVariable[Subscript["ρ", "1"], "MassDensity"] + QuantityVariable[Subscript["ρ", "2"], "MassDensity"])/QuantityVariable["ρ", "MassDensity"]](https://www.wolframcloud.com/objects/resourcesystem/marketplacestorage/resources/758/7586e30a-7c68-4f76-94e3-a010659c17e5/Webpage/FormulaImage.png)

![FormulaData[
ResourceObject[
"Boussinesq Approximation Parameter Using Fluid Densities"], \
{QuantityVariable["Bs","BoussinesqApproximationParameter"] -> 0.01`,
QuantityVariable["\[Rho]","MassDensity"] ->
Quantity[1.`, ("Grams")/("Centimeters")^3]}]](images/758/7586e30a-7c68-4f76-94e3-a010659c17e5-io-3-i.en.gif)